2021年安徽选调生考试冲刺模拟：数量关系（3.25）

发布时间：2021-03-25 09:18 | 安徽政道公务员 | 咨询QQ

微信群

　　1.某工程由小张、小王两人合作刚好可在规定的时间内完成。如果小张的工作效率提高 20%，那么两人只需用规定时间的 9/10 就可完成工程;如果小王的工作效率降低 25%，那么两人就需延迟 2.5 小时完成工程。问规定的时间是多长?( )

　　A.20小时

　　B.24小时

　　C.26小时

　　D.30小时

　　2.已知一对幼兔能在一月后长成一对成年兔子，一对成年兔子能在一个月后生出一对幼兔，如果现在给你一对幼兔，问一年后共有( )对兔子。(假设每对兔子都为雌雄各一只)。

　　A.88

　　B.100

　　C.144

　　D.204

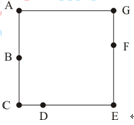
　　3.已知在如下图所示的正方形ACEG的边界上有7个点A、B、C、D、E、F、G，其中B、D、F分别在边AC、CE、EG上。如果以这7个点的4个点为顶点组成的不同的四边形共有多少个?

　　A.23

　　B.27

　　C.31

　　D.35

　　4.甲乙两个工程队共同修建一段长为2100千米的公路，甲队每天比乙队少修50千米，甲队先单独修3天，余下的路程与乙队合修6天完成，则乙队每天所修公路的长度是

　　A.135千米

　　B.140千米

　　C.160千米

　　D.170千米

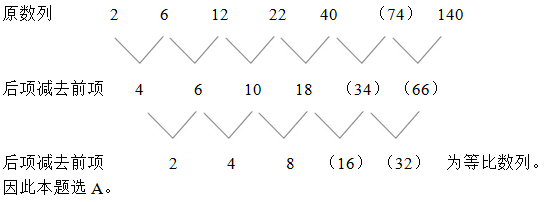
　　5.2，6，12，22，40，( )，140

　　A.74

　　B.76

　　C.84

　　D.96

　　答案与解析

　　1.答案: A

　　解析:

　　由小张工作效率提高后两人完成工程的时间只用原来的9/10，可知提高效率前后的效率之比为9：10，也即两个人合作的效率提高了1/9。假定小张原来的工作效率为5，则现在提高了20%，也即效率增加了1，而增加的1占两人原合作效率的1/9，所以两人合作效率为9，于是可知小王的效率为4。而小王的工作效率降低25%，也即减少1，则两个人的合作效率变为8，前后效率之比为9：8，从而可知完成时间之比为8：9(这说明若规定时间看做8份的话，则现在要用的时间是9份，比原来多出1份)，而题目给出延迟2.5小时，于是可知规定时间为2.5×8=20小时。故正确答案为A。

　　2.答案: C

　　解析: 设第N月有a1只能生的兔子a2只不能生的兔子，则共有兔子(a1+a2);第N+1月有(a1+a2)(能生)+a1(不能生)只兔子;第N+2月有(a1+a2)(能生)+(a1+a2)(不能生)+a1(能生)，明显第N+2月的兔子对数等于第N月与第N+1月的数量之和，因此各月的兔子对数依次为递推和数列。第一个月兔子对数为1对，第二个月兔子对数为,1对，第三个月为2对…按照简单递推和数列写出即为1，1，2，3，5，8，13，21，34，55，89，144。第12个月的兔子总数为144只。因此本题正确答案为C。

　　3.答案: A

　　解析: 根据题意，从7个点中选出4个点共有